Heat transfer in falling-film boiling
The correlation of Kunz and Yerazunis (H. R. Kunz and S. Yerazunis, An Analysis of Film Condensation, Film Evaporation, and Single-Phase Heat Transfer for Liquid Prandtl Numbers From 0.001 to 10000, J. Heat Transfer / Volume 91 / Issue 3, 413-421, doi:10.1115/1.3580203 (?)), also cited in Perry, Chemical Engineers Handbook 7th ed. page 11-16 can be used to predict the heat transfer coefficient for falling-film evaporators.
The correlation is presented in the form of a graph, which makes its application in a computer system unpractical:
This graph can be digitized using the excellent utility ScanIt. The resulting digitized plot can be fitted using gnuplot to this expression:
a(x) = ((aa*x + ab)*x + ac)
b(x) = ((ba*x + bb)*x + bc)
c(x) = ((ca*x + cb)*x + cc)
d(x) = ((da*x + db)*x + dc)
e(x) = (ea*x + eb)
f(x) = (fa*x + fb)
g(x,y) = (a(y)*x+b(y))*(0.5-atan((x-e(y))*f(y))/3.14159265)+(c(y)*x+d(y))*(atan((x-e(y))*f(y))/3.14159265+0.5)
The expression g(x,y) returns the base-10 logarithm of the graph abscissa h / (K^3*rho^2*g/mu^2)^(1/3) as a function of:
- 1 < x = log10(Re) < 5
- 0 < y=log10(Pr) < 3.
The numerical values for the coefficients are:
| aa | -0.112754 |
| ab | 0.047577 |
| ac | -0.613718 |
| ba | 0.197783 |
| bb | -0.0809519 |
| bc | 0.614201 |
| ca | -0.00307804 |
| cb | 0.0140499 |
| cc | 0.290747 |
| da | 0.0255274 |
| db | 0.127306 |
| dc | -1.0811 |
| ea | -1.15207 |
| eb | 2.44218 |
| fa | 0.286347 |
| fb | 0.439599 |
The expression is smooth and qualitatively reproduces the original plot:
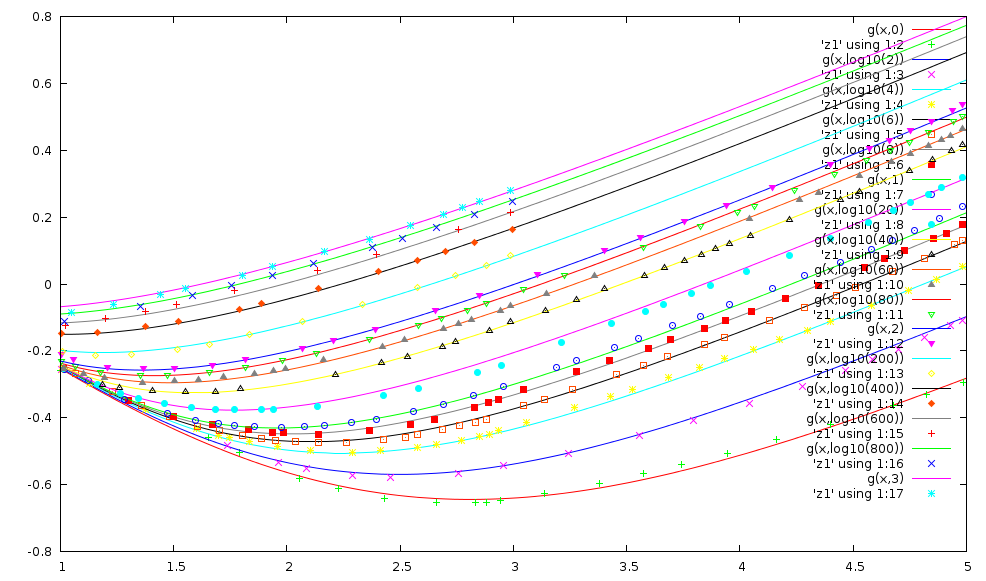 The deviation in term of graph abscissa are on average 1.2%, and less than 1% for more than half of the sampled points (370).
The deviation in term of graph abscissa are on average 1.2%, and less than 1% for more than half of the sampled points (370).
