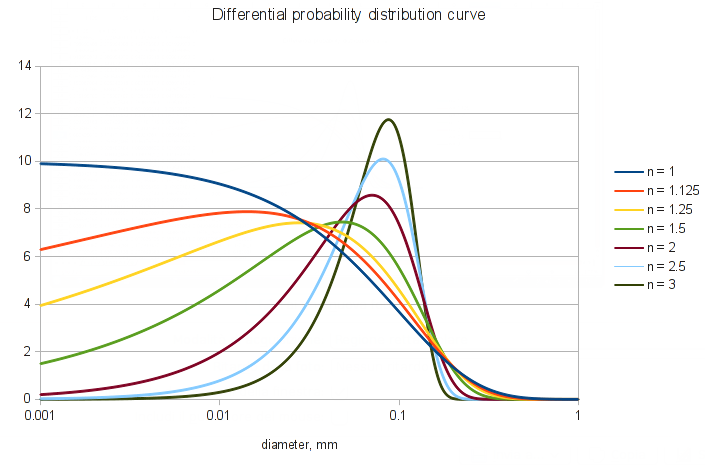
The RRSB particle size distribution
In the concrete and coal processing industries the RRSB (Rosin, Rammler, Sperling und Bennett) equation for interpolating PSD (Particle Size Distribution) curves is quite popular. The RRSB distribution is:
D=1-exp(-(d/d’)^n)
and has this appearance:
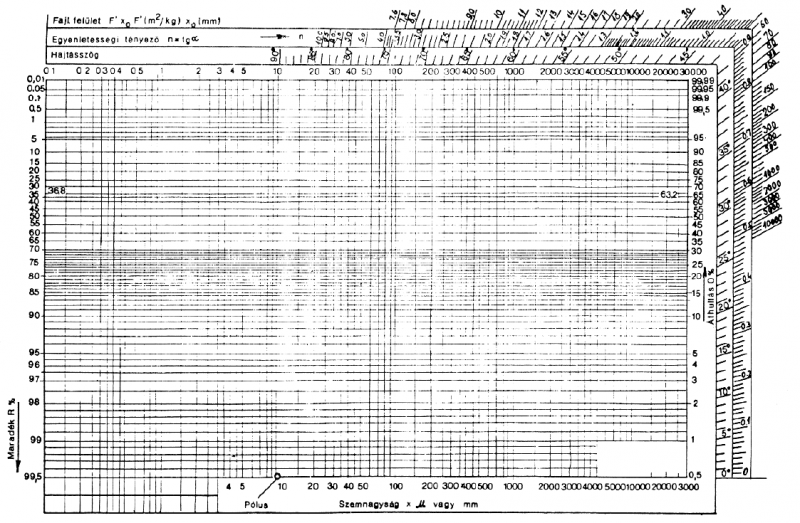
The name RRSB is used in the tecnical norm DIN 66145 , “Darstellung von Korn-(Teilchen-)größenverteilungen – RRSB-Netz” (“Graphical representation of particle size distributions; RRSB-grid“) which presents a curious grid:
The grid is based on log vs. log-log scales and is such that if the experimental measurements from a sieve analysis are drawn on it, and a linear interpolation is used, the resulting curve has the form of the RRSB equation above.
Indeed that can be rewritten:
ln(1-D)= -(d/d’)^n
now calling Y=ln(1-D) it becomes:
Y= -(d/d’)^n
that’s why it appears like a straight line on the log vs. log-log plot (y = x^n curves are straight lines on a log vs. log plot).
At first sight it is easy to oversee the fact that the y axis is on a log-log scale rather than just a log-scale. If you look at low D values (right axis in the figure above, it looks like a plain log-scale (because for D small ln(1-D) is almost the same as D). But the distance between the decades increases at values of D approaching 1, which hints at its log-log nature.
In non-German-speaking parts of the world and outside of the concrete and coal processing industries, the RRSB curve is more widely known as Weibull distribution. In Microsoft Excel for example you have the function:
WEIBULL(X;Alfa;Beta;Cumulative)
where:
- X is the diameter
- Alfa is the form factor and is the same as n in the expression above
- Beta is the scale factor and is the same as d’ above
- Cumulative can be set to FALSE to obtain the differential probability distribution curve, which is the same as the PSD in particle jargon.
The RRBS i.e. Weibull PSD has been attributed some physical meaning for powders resulting from crushing or grinding processes. It is also used for crystallizates though.